Geometry-Aware Merge Tree Comparisons for Time-Varying Data with Interleaving Distances

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Comparisons.

Fast forward

Keywords

Merge trees, merge tree metrics, topological data analysis, topology in visualization

Abstract

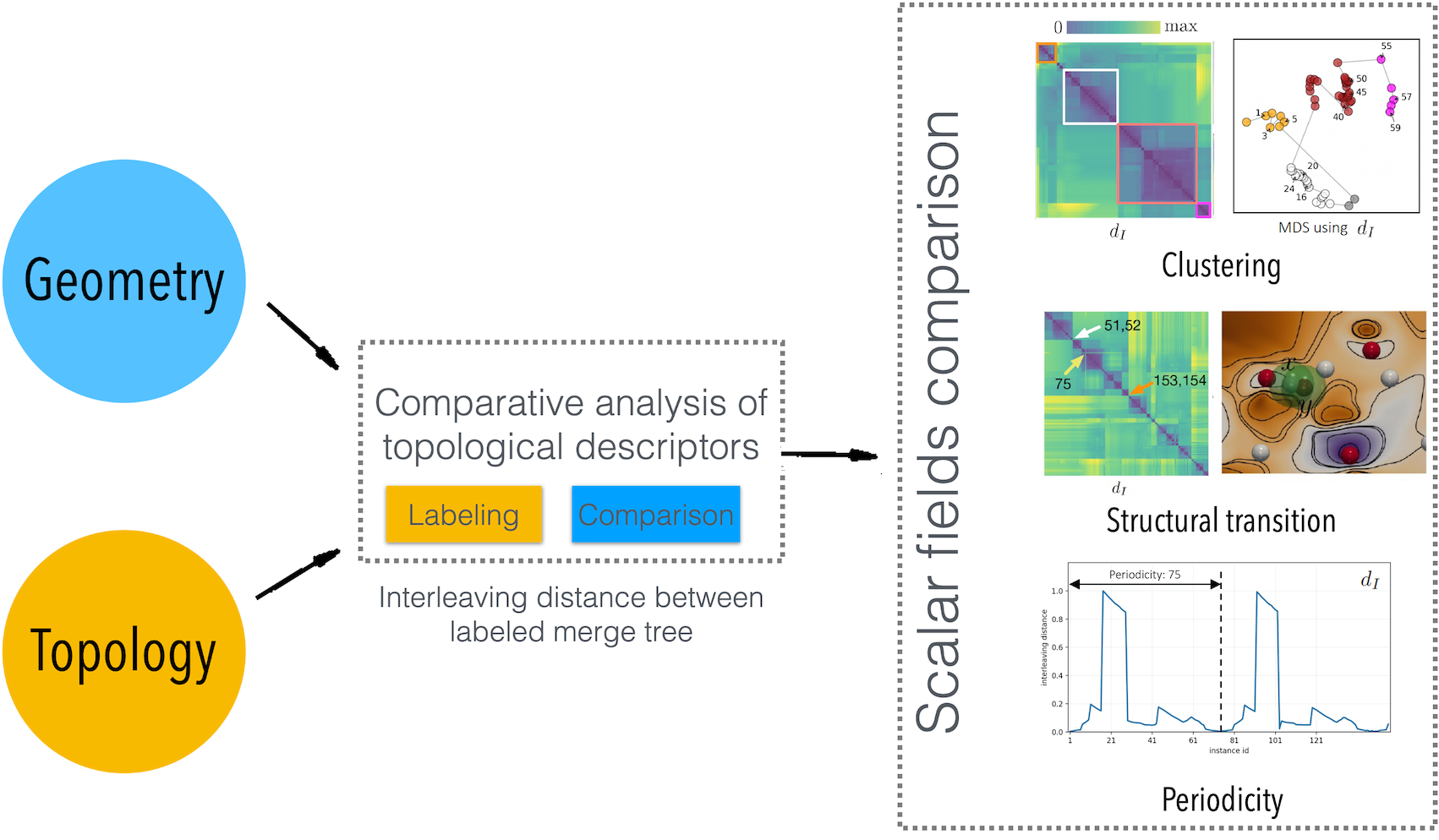
Merge trees, a type of topological descriptor, serve to identify and summarize the topological characteristics associated with scalar fields. They have great potential for analyzing and visualizing time-varying data. First, they give compressed and topology-preserving representations of data instances. Second, their comparisons provide a basis for studying the relations among data instances, such as their distributions, clusters, outliers, and periodicities. A number of comparative measures have been developed for merge trees. However, these measures are often computationally expensive since they implicitly consider all possible correspondences between critical points of the merge trees. In this paper, we perform geometry-aware comparisons of merge trees using labeled interleaving distances. The main idea is to decouple the computation of a comparative measure into two steps: a labeling step that generates a correspondence between the critical points of two merge trees, and a comparison step that computes distances between a pair of labeled merge trees by encoding them as matrices. We show that our approach is general, computationally efficient, and practically useful. Our framework makes it possible to integrate geometric information of the data domain in the labeling process. At the same time, the framework reduces the computational complexity since not all possible correspondences have to be considered. We demonstrate via experiments that such geometry-aware merge tree comparisons help to detect transitions, clusters, and periodicities of time-varying datasets, as well as to diagnose and highlight the topological changes between adjacent data instances.