Visualizing Confidence Intervals for Critical Point Probabilities in 2D Scalar Field Ensembles



Dominik Vietinghoff, Michael Böttinger, Gerik Scheuermann, Christian Heine

 View presentation:2022-10-20T19:36:00ZGMT-0600Change your timezone on the schedule page
2022-10-20T19:36:00Z

Exemplar figure, described by caption below — Confidence intervals for critical point occurrence probabilities for two ensembles of synthetic fields with a different number of members. The red, blue, and green thirds of the glyphs show the confidence intervals for maxima, minima, and saddles at the respective grid points. The area of the darker, inner arcs is proportional to the lower bounds of the found confidence intervals, the area of the lighter, outer arcs to their upper bounds. The black line marks the point estimate for the probability of a critical point of each type computed from the input ensemble.

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Scientific Visualization, Ensembles, and Accessibility.

Fast forward

Keywords

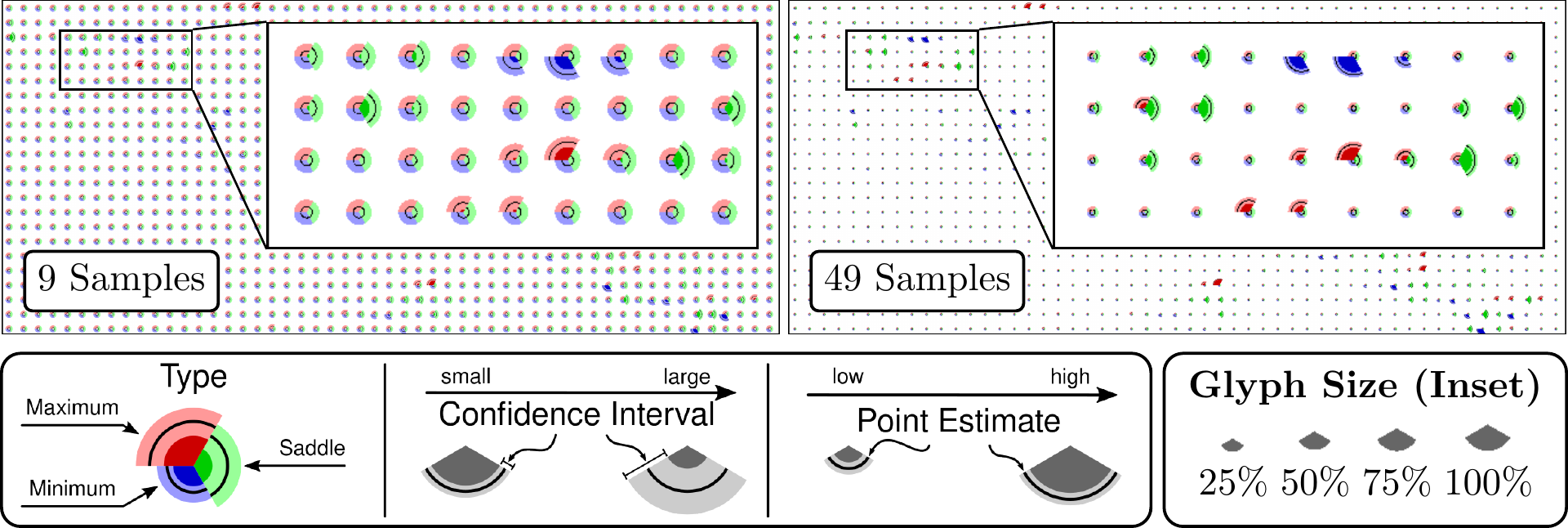
Uncertainty visualization, scalar topology, critical points, ensemble data, climate data, inferential statistics, glyphs.

Abstract

An important task in visualization is the extraction and highlighting of dominant features in data to support users in their analysis process. Topological methods are a well-known means of identifying such features in deterministic fields. However, many real-world phenomena studied today are the result of a chaotic system that cannot be fully described by a single simulation. Instead, the variability of such systems is usually captured with ensemble simulations that produce a variety of possible outcomes of the simulated process. The topological analysis of such ensemble data sets and uncertain data, in general, is less well studied. In this work, we present an approach for the computation and visual representation of confidence intervals for the occurrence probabilities of critical points in ensemble data sets. We demonstrate the added value of our approach over existing methods for critical point prediction in uncertain data on a synthetic data set and show its applicability to a data set from climate research.