MosaicSets: Embedding Set Systems into Grid Graphs

Peter Rottmann, Markus Wallinger, Annika Bonerath, Sven Gedicke, Martin Nöllenburg, Jan-Henrik Haunert

View presentation:2022-10-20T15:45:00ZGMT-0600Change your timezone on the schedule page
2022-10-20T15:45:00Z
Exemplar figure, described by caption below
We present MosaicSets: a novel approach to create Euler-like diagrams from non-spatial set systems such that each element occupies one cell of a regular hexagonal or square grid. The main challenge is to find an assignment of the elements to the grid cells such that each set constitutes a contiguous region. In fact, this task is NP-hard. Thus, we provide an approach using integer linear programming. In the given figure, we visualize the research groups of the Agricultural Faculty of the University of Bonn with MosaicSets once with a hexagonal grid and once with a square grid.

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Graphs and Networks.

Fast forward
Abstract

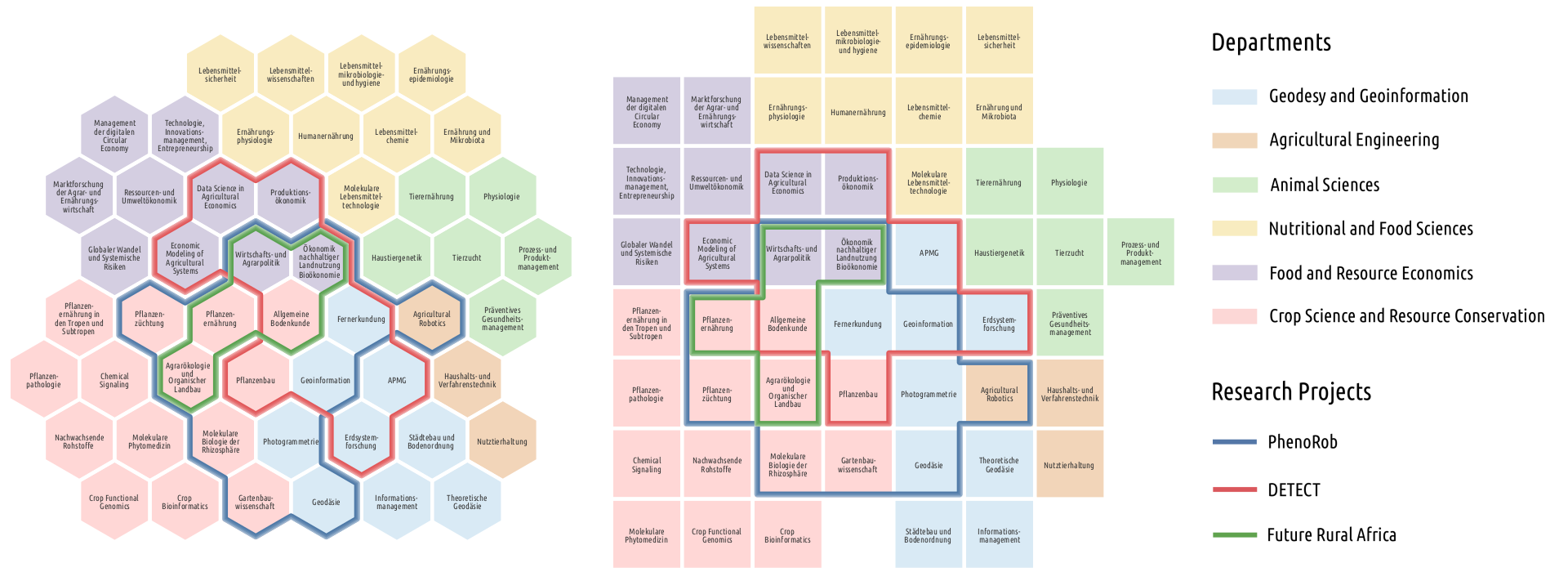
Visualizing sets of elements and their relations is an important research area in information visualization. In this paper, we present MosaicSets: a novel approach to create Euler-like diagrams from non-spatial set systems such that each element occupies one cell of a regular hexagonal or square grid. The main challenge is to find an assignment of the elements to the grid cells such that each set constitutes a contiguous region. As use case, we consider the research groups of a university faculty as elements, and the departments and joint research projects as sets. We aim at finding a suitable mapping between the research groups and the grid cells such that the department structure forms a base map layout. Our objectives are to optimize both the compactness of the entirety of all cells and of each set by itself. We show that computing the mapping is NP-hard. However, using integer linear programming we can solve real-world instances optimally within a few seconds. Moreover, we propose a relaxation of the contiguity requirement to visualize otherwise non-embeddable set systems. We present and discuss different rendering styles for the set overlays. Based on a case study with real-world data, our evaluation comprises quantitative measures as well as expert interviews.