Fiber Uncertainty Visualization for Bivariate Data With Parametric and Nonparametric Noise Models



Tushar M. Athawale, Chris R. Johnson, Sudhanshu Sane, David Pugmire

 View presentation:2022-10-19T20:45:00ZGMT-0600Change your timezone on the schedule page
2022-10-19T20:45:00Z

Exemplar figure, described by caption below — Mean, parametric, and nonparametric noise models for uncertainty analysis of vortical features of the Red Sea ensemble dataset. Fiber positions are visualized for a trait corresponding to anticyclonic (negative Z component of curl) vortices, as indicated by the cyan polygon in image (a). The parametric noise model (c) suggests multiple high-probability vortices inside the magenta box, whereas the mean (b) and nonparametric (d) statistical models suggest a relatively low number of vortices inside the magenta box. Such inconsistency inside the magenta box across the three statistical models indicates the need for further eddy analysis in the same region.

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Uncertainty.

Fast forward

Abstract

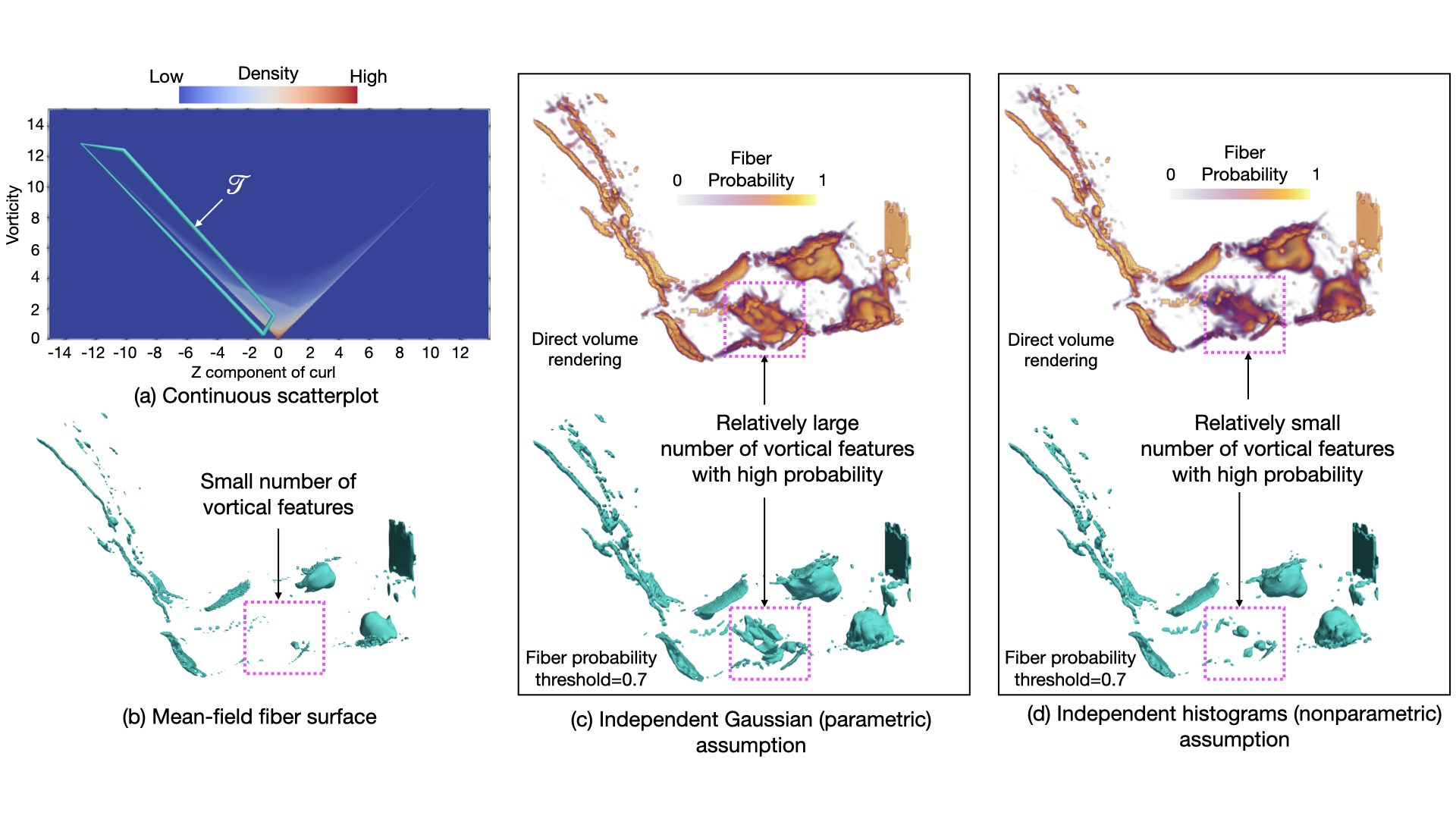
Visualization and analysis of multivariate data and their uncertainty are top research challenges in data visualization. Constructing fiber surfaces is a popular technique for multivariate data visualization that generalizes the idea of level-set visualization for univariate data to multivariate data. In this paper, we present a statistical framework to quantify positional probabilities of fibers extracted from uncertain bivariate fields. Specifically, we extend the state-of-the-art Gaussian models of uncertainty for bivariate data to other parametric distributions (e.g., uniform and Epanechnikov) and more general nonparametric probability distributions (e.g., histograms and kernel density estimation) and derive corresponding spatial probabilities of fibers. In our proposed framework, we leverage Green’s theorem for closed-form computation of fiber probabilities when bivariate data are assumed to have independent parametric and nonparametric noise. Additionally, we present a nonparametric approach combined with numerical integration to study the positional probability of fibers when bivariate data are assumed to have correlated noise. For uncertainty analysis, we visualize the derived probability volumes for fibers via volume rendering and extracting level sets based on probability thresholds. We present the utility of our proposed techniques via experiments on synthetic and simulation datasets.