Computing a Stable Distance on Merge Trees

Prerecorded Talk

The live footage of the talk, including the Q&A, can be viewed on the session page, Topology.

Fast forward

Abstract

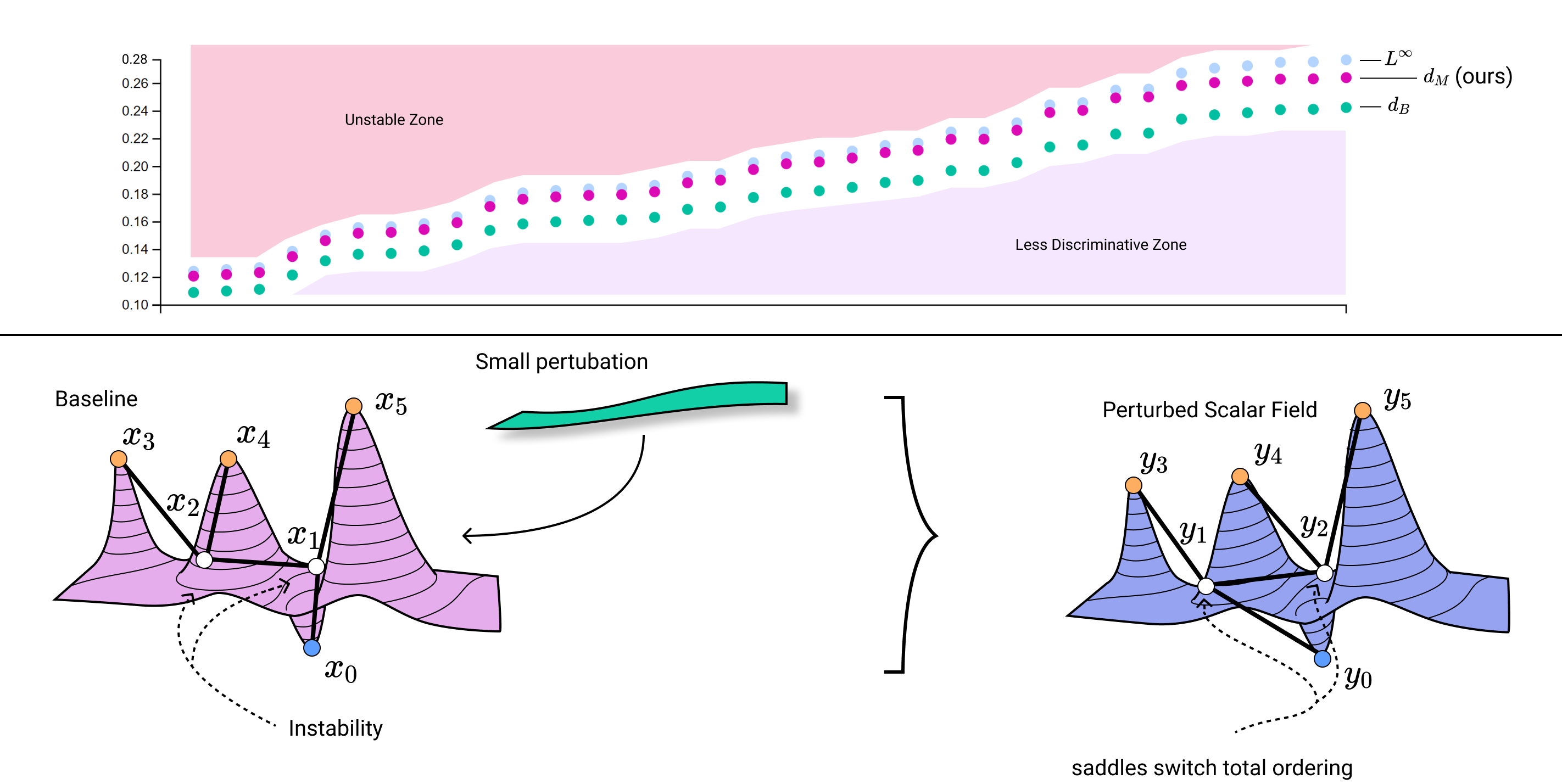
Distances on merge trees facilitate visual comparison of collections of scalar fields. Two desirable properties for these distances to exhibit are 1) the ability to discern between scalar fields which other, less complex topological summaries cannot and 2) to still be robust to perturbations in the dataset. The combination of these two properties, known respectively as stability and discriminativity, has led to theoretical distances which are either thought to be or shown to be computationally complex and thus their implementations have been scarce. In order to design similarity measures on merge trees which are computationally feasible for more complex merge trees, many researchers have elected to loosen the restrictions on at least one of these two properties. The question still remains, however, if there are practical situations where trading these desirable properties is necessary. Here we construct a distance between merge trees which is designed to retain both discriminativity and stability. While our approach can be expensive for large merge trees, we illustrate its use in a setting where the number of nodes is small. This setting can be made more practical since we also provide a proof that persistence simplification increases the outputted distance by at most half of the simplified value. We demonstrate our distance measure on applications in shape comparison and on detection of periodicity in the von Kármán vortex street.