A Scalable Method for Readable Tree Layouts
Kathryn Gray, Mingwei Li, Reyan Ahmed, Md. Khaledur Rahman, Ariful Azad, Stephen Kobourov, Katy Börner
DOI: 10.1109/TVCG.2023.3274572
Room: 105
2023-10-24T23:45:00ZGMT-0600Change your timezone on the schedule page
2023-10-24T23:45:00Z
Fast forward
Full Video
Keywords
Tree layouts;force-directed;readability
Abstract
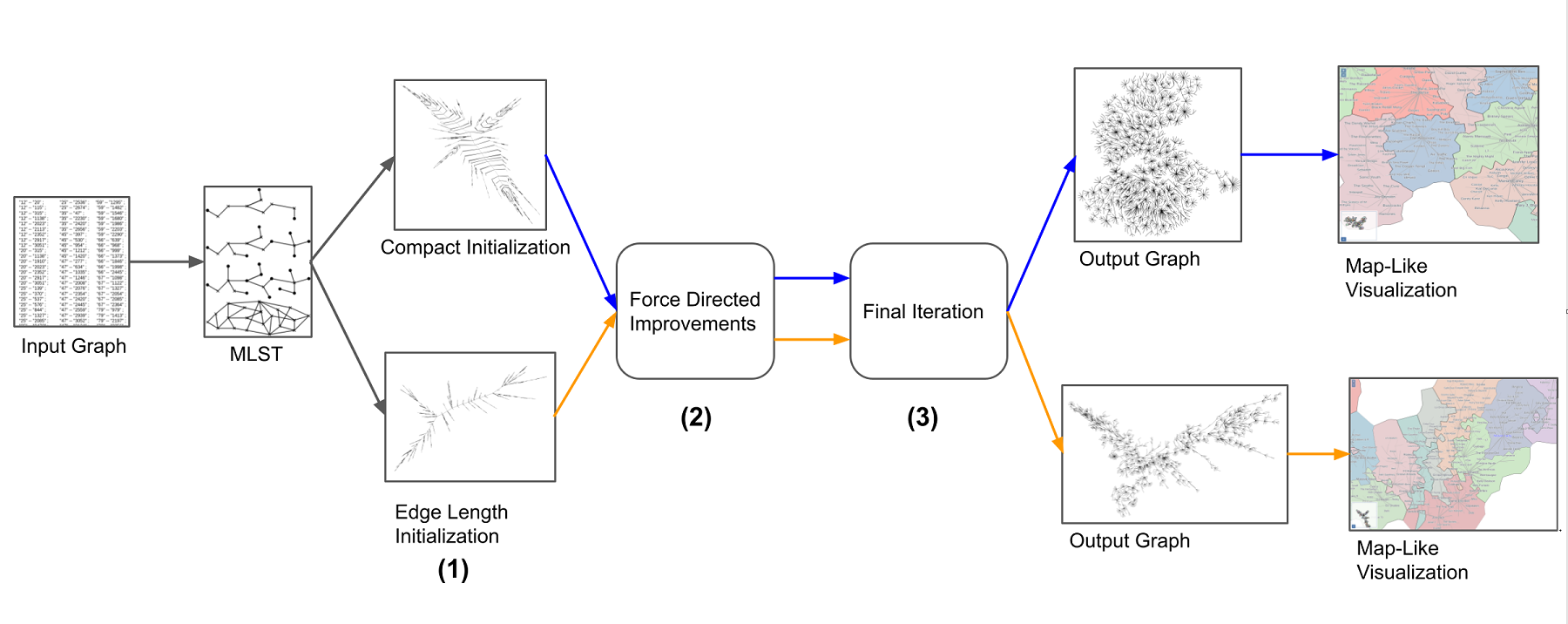
Large tree structures are ubiquitous and real-world relational datasets often have information associated with nodes (e.g., labels or other attributes) and edges (e.g., weights or distances) that need to be communicated to the viewers. Yet, scalable, easy to read tree layouts are difficult to achieve. We consider tree layouts to be readable if they meet some basic requirements: node labels should not overlap, edges should not cross, edge lengths should be preserved, and the output should be compact. There are many algorithms for drawing trees, although very few take node labels or edge lengths into account, and none optimizes all requirements above. With this in mind, we propose a new scalable method for readable tree layouts. The algorithm guarantees that the layout has no edge crossings and no label overlaps, and optimizing one of the remaining aspects: desired edge lengths and compactness. We evaluate the performance of the new algorithm by comparison with related earlier approaches using several real-world datasets, ranging from a few thousand nodes to hundreds of thousands of nodes. Tree layout algorithms can be used to visualize large general graphs, by extracting a hierarchy of progressively larger trees. We illustrate this functionality by presenting several map-like visualizations generated by the new tree layout algorithm.