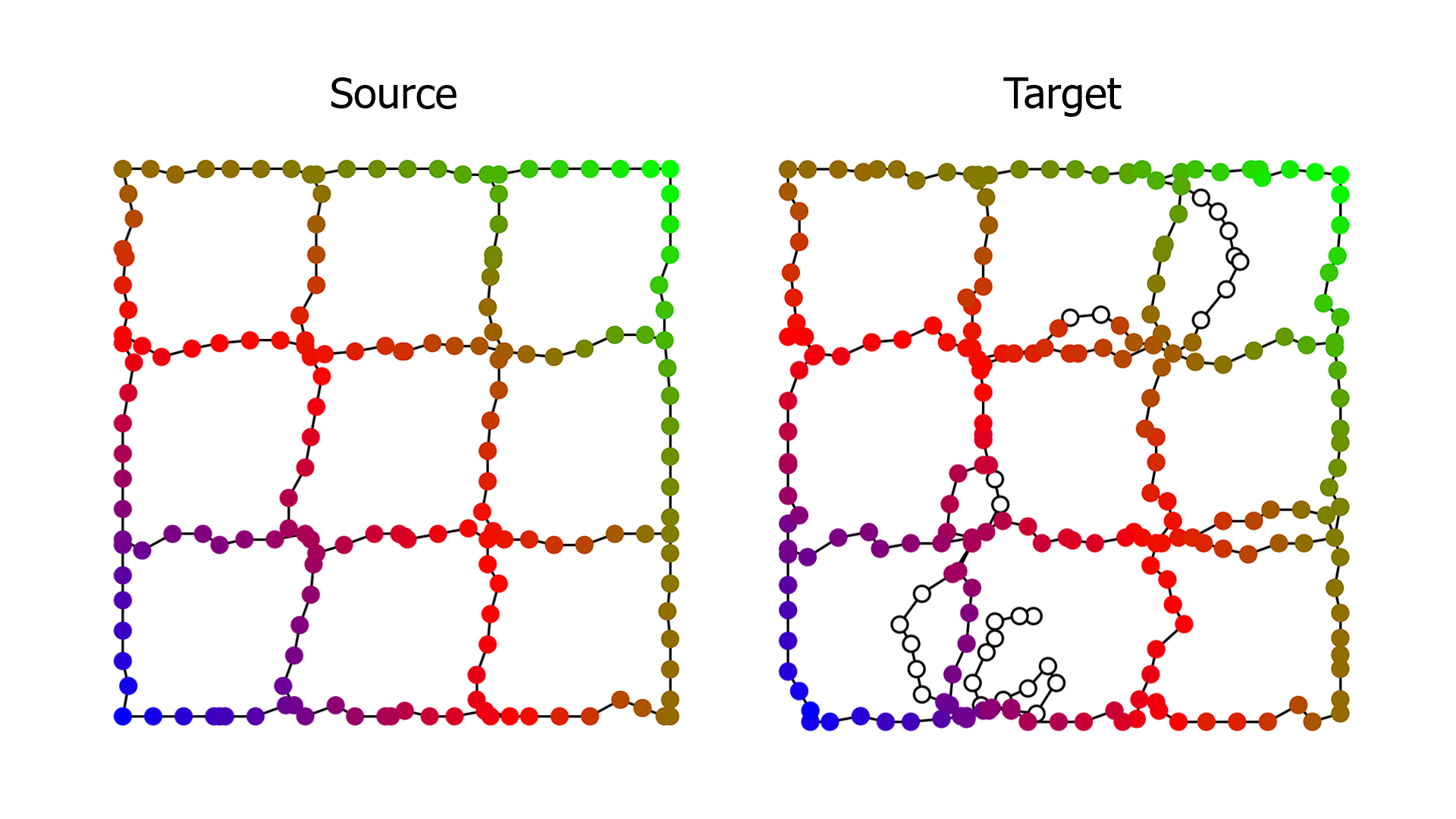
Comparing Morse Complexes Using Optimal Transport: An Experimental Study
Mingzhe Li, Carson Storm, Austin Yang Li, Tom Needham, Bei Wang Phillips
Room: 104
2023-10-24T23:03:00ZGMT-0600Change your timezone on the schedule page
2023-10-24T23:03:00Z
Fast forward
Full Video
Keywords
Morse Complexes, topological data analysis, optimal transport, topology in visualization
Abstract
Morse complexes and Morse-Smale complexes are topological descriptors popular in topology-based visualization. Comparing these complexes plays an important role in their applications in feature correspondences, feature tracking, symmetry detection, and uncertainty visualization. Leveraging recent advances in optimal transport, we apply a class of optimal transport distances to the comparative analysis of Morse complexes. Contrasting with existing comparative measures, such distances are easy and efficient to compute, and naturally provide structural matching between Morse complexes. We perform an experimental study involving scientific simulation datasets and discuss the effectiveness of these distances as comparative measures for Morse complexes. We also provide an initial guideline for choosing the optimal transport distances under various data assumptions.