A Local Iterative Approach for the Extraction of 2D Manifolds from Strongly Curved and Folded Thin-Layer Structures

Fast forward

Full Video

Keywords

Ridge surface, crease surface, 2D manifold extraction, fast marching, virtual unfolding, historical documents

Abstract

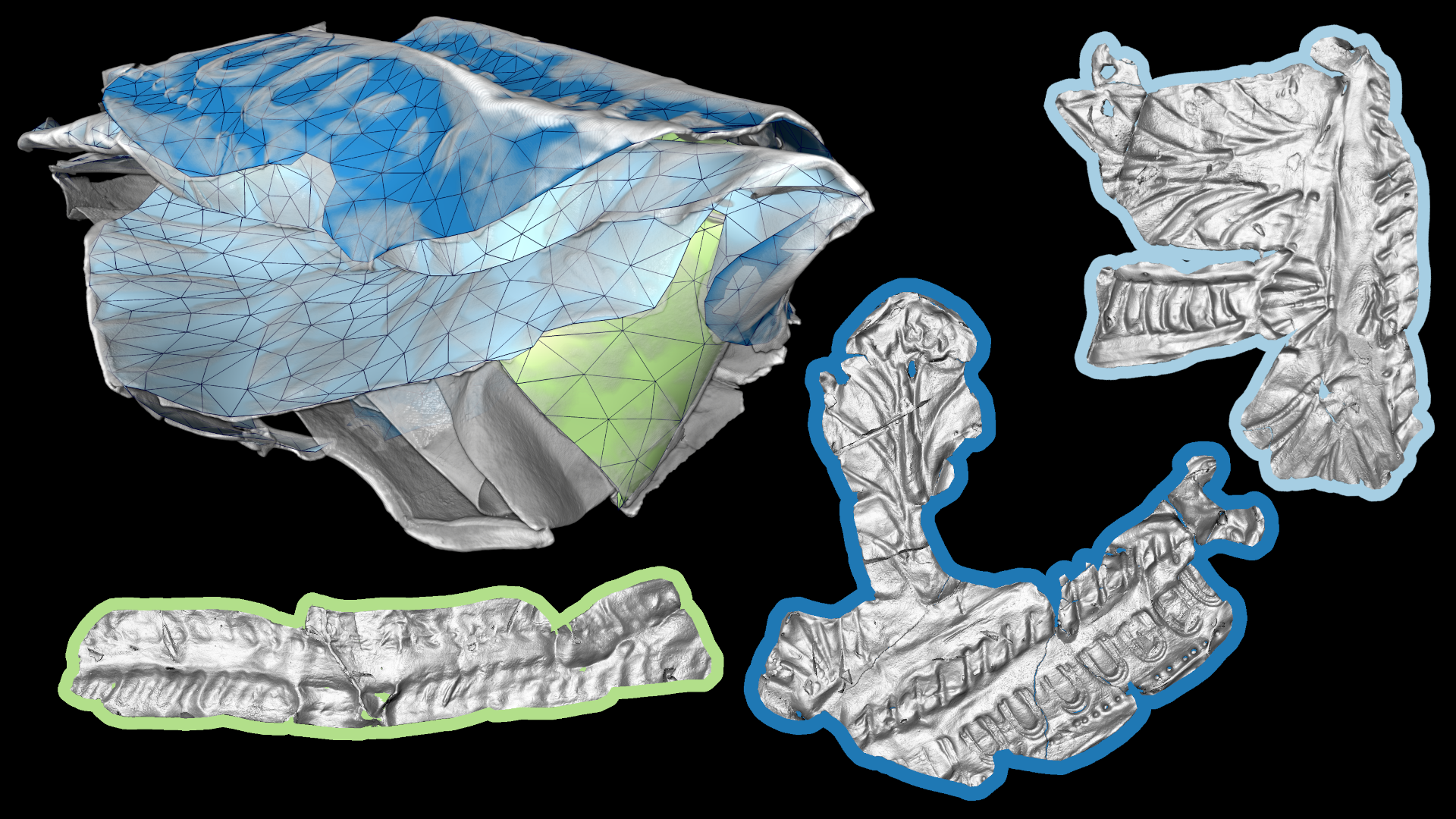
Ridge surfaces represent important features for the analysis of 3-dimensional (3D) datasets in diverse applications and are often derived from varying underlying data including flow fields, geological fault data, and point data, but they can also be present in the original scalar images acquired using a plethora of imaging techniques. Our work is motivated by the analysis of image data acquired using micro-computed tomography (μCT) of ancient, rolled and folded thin-layer structures such as papyrus, parchment, and paper as well as silver and lead sheets. From these documents we know that they are 2-dimensional (2D) in nature. Hence, we are particularly interested in reconstructing 2D manifolds that approximate the document’s structure. The image data from which we want to reconstruct the 2D manifolds are often very noisy and represent folded, densely-layered structures with many artifacts, such as ruptures or layer splitting and merging. Previous ridge-surface extraction methods fail to extract the desired 2D manifold for such challenging data. We have therefore developed a novel method to extract 2D manifolds. The proposed method uses a local fast marching scheme in combination with a separation of the region covered by fast marching into two sub-regions. The 2D manifold of interest is then extracted as the surface separating the two sub-regions. The local scheme can be applied for both automatic propagation as well as interactive analysis. We demonstrate the applicability and robustness of our method on both artificial data as well as real-world data including folded silver and papyrus sheets.